Develop a new mechanism (protocol)

Developing a new mechanism for NegMAS is as easy as overriding a single method. In most cases though, a base class for negotiators compatible with this protocol needs to be created.

The algorithm for creating a new mechanism in NegMAS is simple:

1. Create a new Mechanism class and override the round() method to implement a single round of your protocol. Optionally override the __init__ function to provide a constructor to initialize your mechanism. Define any requirements of your mechanism that must be satisfied by negotiators using add_requirements() during construction (i.e. in the __init__ method).

2. Create a new Negotiator class that has abstractmethod(s) for any methods called by your custom mechanism class (usually in the round() method). This will be the base class of all negotiators compatible with this new mechanism. Set any capabilities for this new negotiator base class in its __init__ method using add_capabilities()

3. Optionally create a new MechanismState dataclass with any extra state information that the mechanism will pass to negotiators and override the extra_state() method of your mechanism class to return a dict representation of this extra state (you will see an example later in this tutorial). Moreover, you will need to change the state_factory argument passed to the Mechechanism constructor to use this newly created state type. This step is optional and is only needed if extra-state needs to be passed to negotiators through the state method. It t is recommended to keep all variable publicly accessible information of the mechanism in its state variable. This way, the history of the mechanism state will be accessible through the history property after the mechanism run.

Nash Bargaining Game (Stateless Mechanism)

Let’s start by developing one of the earliest negotiation protocols every proposed: Nash Bargaining Game (1950) .

The Nash bargaining game is a single-step full-information bilateral negotiation with \(\Omega = [0, 1]^2\) and two utility functions (\(\tilde u_1, \tilde u_2\)) such that: - A (usually convex) feasible set of agreements \(F\). A common example is to define \(F\) as all the outcomes for which the total utility received by negotiators is less than or equal to one:

\[F = \left\{(\omega_1, \omega_2) | \tilde u_2(\omega_2) + \tilde u_1(\omega_1) \le 1\right\}\]

.

• A disagreement point \(d \equiv \tilde u_1(\phi) + \tilde u_2(\phi) \in \Re^2\) which is the utility value received by the two players in case of disagreement ( reserved values) and \(\phi\) represents the disagreement.

class NashBargainingGame(Mechanism):
    """A mechanism representing the nash bargaining game"""

    def __init__(self, **kwargs):
        kwargs.update(dict(n_steps=1, max_n_agents=2, dynamic_entry=False))
        super().__init__(**kwargs, issues=[make_issue((0.0, 1.0))])
        self.add_requirements(dict(propose_for_self = True))
        self.ufuns: List[UtilityFunction] = []

    def add(
        self,
        negotiator: "Negotiator",
        *,
        preferences: Optional["Preferences"] = None,
        **kwargs,
    ) -> Optional[bool]:
        added = super().add(negotiator, preferences=preferences, role=None, **kwargs)
        if added:
            self.ufuns.append(self.negotiators[-1].ufun)

    def is_feasible(self, outcome: Tuple[float]):
        """Tests feasibility of outcomes.

        The default implementation tests that the of all utilities assigned to all negotiators is less than 1.0.
        """
        return sum(u(outcome) for u in self.ufuns) <= (1.0 + 1e-3)

    def round(self)-> MechanismRoundResult:
        """One round of the mechanism"""
        if len(self.negotiators) != 2:
            return MechanismRoundResult(error=True,
                                        error_details=f"Got {len(self.negotiators)} negotiators!!",
                                        broken=True)
        outcome = tuple(n.propose_for_self(self.ufuns, i) for i, n in enumerate(self.negotiators))
        if self.is_feasible(outcome):
            return MechanismRoundResult(agreement=outcome)
        return MechanismRoundResult()

The implementation is straight forward. We need to define what a round of the algorithm does (round() ). In this case we used is_feasible() to distinguish feasible and infeasible outcomes.

We need now to develop a base class for negotiators compatible with this mechanism.

class NashBargainingNegotiator(Negotiator, ABC):
    """Base class of all negotiators capable of negotiating in the nash bargaining game"""

    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.add_capabilities(dict(propose_for_self=True))

    @abstractmethod
    def propose_for_self(self, ufuns: List[UtilityFunction], my_indx: int) -> float:
        """Propose some outcome which is just a real number"""

Note that any agreement with utilities that sum to the maximum possible value within the feasible space is a nash equilibrium to this game and is pareto-efficient.

Based on the axioms used to represent rationality, there are three widely known equilibria for the Nash bargaining game:

• Nash Point (1950): The point at which the product of surplus utility (above reservation value) of negotiators is maximized

\[\text{argmax}_{\omega_1, \omega_2} \prod_{i=1}^2\left(\tilde u_i(\omega_{i}) - \tilde u_i(\phi)\right)\]

• Kalai-Smorodinsky Point (1975): The pareto outcome with equal ratios of achieved surplus utility and maximum feasible surplus utility

\[\text{argmax}_{\omega_1, \omega_2 \in F}\left(\omega_1+\omega_2\right) \text{ s.t. } \left(\frac{\tilde u_1(\omega_1)-\tilde u_1(\phi)}{\tilde u_2(\omega_2)-\tilde u_2(\phi)} = \frac{\max_{v \in F} \left(\tilde u_1(v)\right)-\tilde u_1(\phi)}{\max_{v \in F} \left(\tilde u_2(v)\right)-\tilde u_2(\phi)}\right)\]

• Kalai Point (1977): The pareto outcome maximizing the utility for the unfortunate player. Defining \(P\) as the pareto front,

\[\text{argmax}_{\omega_1, \omega_2 \in P} \min_{i \in \{1,2\}}\left(\tilde u_i(\omega_{i}) - \tilde u_i(\phi)\right)\]

We will not implement a negotiator that plays he nash-point strategy with no prior knowledge of the utility function structure (i.e. it works for nonlinear nonconvex utility functions).

class NashNegotiator(NashBargainingNegotiator):
    """Implements Nash solution to the bargaining game"""
    def propose_for_self(self, ufuns: List[UtilityFunction], my_indx: int)-> float:
        objective = lambda f0: - (ufuns[0]((f0, 1.0-f0)) - ufuns[0].reserved_value) * \
                                 (ufuns[1]((f0, 1.0-f0)) - ufuns[1].reserved_value)
        while True:
            result = minimize(objective, x0=[random()], bounds=[(0.0, 1.0)])
            if result.success:
                break
        return float(result.x) if my_indx == 0 else 1.0 - float(result.x)

Now let’s try our brand new mechanism and negotiator

m = NashBargainingGame()
u1 = LinearUtilityFunction([1, 0], reserved_value=0.0, outcome_space=m.outcome_space)
u2 = LinearUtilityFunction([0, 1], reserved_value=0.0, outcome_space=m.outcome_space)
m.add(NashNegotiator(ufun=u1, name="a1"))
m.add(NashNegotiator(ufun=u2, name="a2"))
result = m.run()
print(f"Agreement: {result.agreement}")

Agreement: (0.500000002718769, 0.5000000054101424)

As expected, the two negotiators agreed on the expected nash point (0.5, 0.5) from the first trial.

It is possible to see what happens at different other conditions. For example, how does the reservation value affect the outcome:

u1values, u2values = np.zeros(101), np.zeros(101)
a1values, a2values = np.zeros(101), np.zeros(101)
values = np.linspace(0.0, 1.0, 101, endpoint=True)
for i, r in enumerate(values):
    m = NashBargainingGame()
    u1 = LinearUtilityFunction([1, 0], reserved_value=r, outcome_space=m.outcome_space)
    u2 = LinearUtilityFunction([0, 1], reserved_value=0.0, outcome_space=m.outcome_space)
    m.add(NashNegotiator(ufun=u1, name="a1"))
    m.add(NashNegotiator(ufun=u2, name="a2"))
    result = m.run()
    u1values[i] =u1(result.agreement)
    u2values[i] =u2(result.agreement)
    a1values[i], a2values[i] = result.agreement
plt.subplot(211)
plt.plot(values, u1values, label="First negotiator")
plt.plot(values, u2values, label="Second negotiator")
plt.plot(values, u1values+u2values, label="Welfare")
plt.ylabel("Utility received")
plt.legend()
plt.xlabel("Reservation value for first negotiator")
plt.show()

plt.subplot(212)
plt.plot(values, a1values, label="First negotiator")
plt.plot(values, a2values, label="Second negotiator")
plt.ylabel("Agreement Reached")
plt.legend()
plt.xlabel("Slope value for first negotiator")
plt.show()

We can see that increasing the reservation value of a negotiator increases the utility it receives by the end of the negotiation proportionally.

What happens if the utility value of a negotiator had a different slope:

u1values, u2values = np.zeros(101), np.zeros(101)
a1values, a2values = np.zeros(101), np.zeros(101)
slopes = np.linspace(0.0, 1.0, 101, endpoint=True)
for i, s in enumerate(slopes):
    m = NashBargainingGame()
    u1 = LinearUtilityFunction([s, 0.0], reserved_value=0.0, outcome_space=m.outcome_space)
    u2 = LinearUtilityFunction([0, 1], reserved_value=0.0, outcome_space=m.outcome_space)
    m.add(NashNegotiator(ufun=u1, name="a1"))
    m.add(NashNegotiator(ufun=u2, name="a2"))
    result = m.run()
    u1values[i], u2values[i] =u1(result.agreement), u2(result.agreement)
    a1values[i], a2values[i] = result.agreement

plt.subplot(211)
plt.plot(slopes, u1values, label="First negotiator")
plt.plot(slopes, u2values, label="Second negotiator")
plt.plot(slopes, u1values+u2values, label="Welfare")
plt.ylabel("Utility received")
plt.legend()
plt.xlabel("Slope value for first negotiator")
plt.show()

plt.subplot(212)
plt.plot(slopes, a1values, label="First negotiator")
plt.plot(slopes, a2values, label="Second negotiator")
plt.ylabel("Agreement Reached")
plt.legend()
plt.xlabel("Slope value for first negotiator")
plt.show()

Notice that in this case, the both negotiators always get their maximum possible utility which leads to a linear increas in welfare with slope. There is a small exception though at slope zero. Try running the last simulation several times. Does the peculiar result at slope zero persist? Does it lead to the same welfare every time? Can you explain it?

Rubinstein Bargaining Protocol (Stateful Mechanism)

Rubinstein provided one of the earliest and most widely cited results for multi-round bilateral negotiation.

In this protocol, two negotiators are again trying to find an agreement each maximizing its own utility. This is a full information game in which the utility function of both agents is common knowledge. Moreover, there is some discount mechanism that reduces the utility of any potential agreement over time which is different for the two negotiators but is also known. In this tutorial we will focus on the case with exponential discounting (with with \(t\) representing round number and \(\delta_i\) is the discount factor for negotiator \(i\)). Throughout this section we will use superscripts to indicate round number. Moreover, we will focus on the case where the initial utility of an agreement is the value assigned to the agent in that agreement:

\[\tilde u_i^t(\omega) = \delta_i^t \omega_i\]

We can start by designing the MechanismState class corresponding to this information.

@dataclass
class RubinsteinMechanismState(MechanismState):
    discounts: Tuple[float, float] = (1.0, 1.0)

We can then define the mechanism class itself:

class RubinsteinMechanism(Mechanism):
    """Simplified Rubinstein's Mechanism with Exponential discounting"""
    def __init__(self, extended=False, **kwargs):
        kwargs.update(dict(issues=[make_issue(values=(0.0, 1.0), name="first")
                                   , make_issue(values=(0.0, 1.0), name="second")],
                                   max_n_agents=2, dynamic_entry=False,
                           state_factory=RubinsteinMechanismState))
        super().__init__(**kwargs)
        self.add_requirements(dict(propose=True, set_index=True))
        self.discounts: List[UtilityFunction] = []
        self.proposals = []
        self.extended = extended

    def extra_state(self) -> Optional[Dict[str, Any]]:
        return dict(discounts=self.discounts)

    def add(
        self,
        negotiator: "Negotiator",
        *,
        discount: float =0.95,
        **kwargs,
    ) -> Optional[bool]:
        weights = [1, 0] if len(self.negotiators) == 0 else [0, 1]
        ufun = ExpDiscountedUFun(
            LinearUtilityFunction(weights, outcome_space=self.outcome_space),
            outcome_space=self.outcome_space, discount=discount
        )
        added = super().add(negotiator, ufun=ufun, role=None, **kwargs)
        if added:
            self.discounts.append(discount)

    def round(self)-> MechanismRoundResult:
        """One round of the mechanism"""
        if self.current_step == 0:
            if len(self.negotiators) != 2:
                return MechanismRoundResult(error=True,
                                        error_details=f"Got {len(self.negotiators)} negotiators!!",
                                        broken=True)
            for i, n in enumerate(self.negotiators):
                n.set_index(i)
        outcomes = list(n.propose(self.state) for n in self.negotiators)
        self.proposals.append(outcomes)
        if any(o is None for o in outcomes):
            return MechanismRoundResult(broken=True)
        if sum(outcomes[0]) <= 1 + 1e-3:
            if self.extended:
                if outcomes[0][0] <= outcomes[1][0] + 1e-5 and outcomes[1][1] <= outcomes[0][1] + 1e-5:
                    return MechanismRoundResult(agreement=(min(outcomes[0][0], outcomes[1][0]),
                                                   min(outcomes[0][1], outcomes[1][1])))
            elif max(abs(outcomes[0][i] - outcomes[1][i]) for i in range(2)) < 1e-3:
                return MechanismRoundResult(agreement=tuple(0.5 *(outcomes[0][i]+outcomes[1][i])
                                                            for i in range(2)))

        return MechanismRoundResult()

The mechanism is very similar to the Nash Bargaining Game with few modifications:

1. The constructor passes the RubnisteinMechanismState as the state_factory. We also create explicit issues for the negotiation. The number of steps is not limited to \(1\). Note that we define two requirements for any negotiator that wants to engage in this protocol.

2. The add() method now creates the utility function for the negotiator following the rules of the game. Each negotiator receives an exponentially discounted utility function of the portion it receives from the pie.

3. We override extra_state to provide the discounts values to the state factory.

4. propose() in the negotiators is expected to receive a state of type RubinsteinMechanismState .

5. Each round all negotiators propose outcomes and the negotiation terminates with success only if both proposals are feasible (sum to no more than 1.0) and equal (approximately)

We can now develop the base negotiator type for this mechanism:

class RubinsteinNegotiator(Negotiator):

    def __init__(self, *args, **kwargs):
        super().__init__(*args, **kwargs)
        self.add_capabilities(dict(propose=True, set_index=True))
        self.my_index = -1

    def set_index(self, indx: i) -> None:
        self.my_index = indx

    @abstractmethod
    def propose(self, state: RubinsteinMechanismState)  -> Outcome:
        """Proposes an outcome which is a tuple of two numbers between zero and one"""

The base negotiator here implements set_index so that specific negotiators need not bother about it. It defines a single abstract method to be overriden by any compatible negotiator.

We will first define a utility function to plot what happens in a negotiation

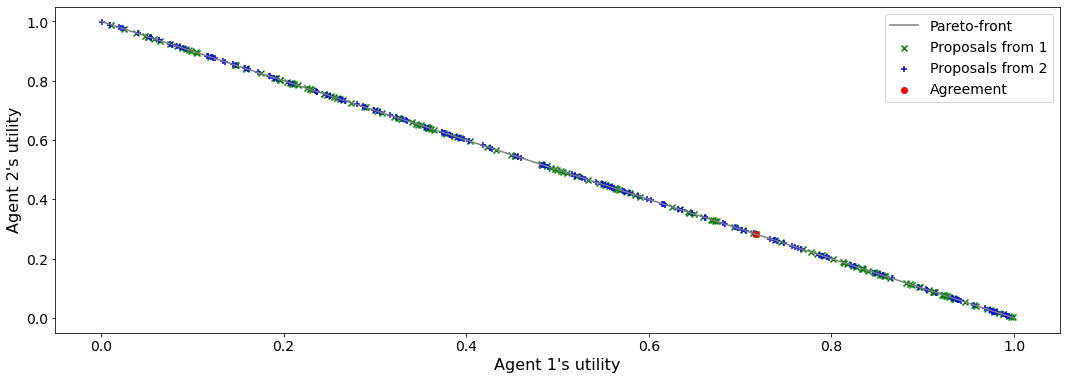
def plot_a_run(mechanism: RubinsteinMechanism) -> None:
    result = mechanism.state
    x = np.linspace(0.0, 1.0, 101, endpoint=True)
    first = np.array([_[0] for _ in mechanism.proposals])
    second = np.array([_[1] for _ in mechanism.proposals])
    plt.plot(x, 1-x, color="gray", label="Pareto-front")
    plt.xlabel("Agent 1's utility")
    plt.ylabel("Agent 2's utility")
    plt.scatter(first[:, 0], first[:, 1], marker="x", color="green", label="Proposals from 1")
    plt.scatter(second[:, 0], second[:, 1], marker="+", color="blue", label="Proposals from 2")
    if result.agreement is not None:
        plt.scatter([result.agreement[0]], [result.agreement[1]], marker="o", color="red", label="Agreement")
    plt.legend()
    plt.show()

Let’s implement a random negotiator that ends the negotiation if it finds that it is impossible to get a positive utility anymore (due to discounting) and otherwise returns a random apportionment of the pie.

class RandomRubinsteinNegotiator(RubinsteinNegotiator):

    def propose(self, state: RubinsteinMechanismState)-> Outcome:
        if self.ufun((1.0, 1.0)) < 0.0:
            return None
        r = random()
        return r, 1 - r

Now we can run negotiations using our new protocol and negotiator:

mechanism = RubinsteinMechanism(extended=False)
mechanism.add(RandomRubinsteinNegotiator(), discount=0.75)
mechanism.add(RandomRubinsteinNegotiator(), discount=0.75)
print(f"Agreed to: {mechanism.run().agreement} after {mechanism.current_step} steps")
plot_a_run(mechanism)

Agreed to: (0.7173821399310416, 0.28261786006895845) after 174 steps

Rubinstein showed in 1982 that there is a single perfect game equilibrium of single round that takes the form:

\[\left(\frac{1-\delta_2}{1-\delta_1\delta_2}, \frac{\delta_2\left(1-\delta_1\right)}{1-\delta_1\delta_2}\right)\]

We can implement the optimal negotiator for this mechanism as follows:

class OptimalRubinsteinNegotiator(RubinsteinNegotiator):

    def propose(self, state: RubinsteinMechanismState) -> Outcome:
        first = (1-state.discounts[1]) / (1 - state.discounts[1] * state.discounts[0])
        return first, 1 - first

mechanism = RubinsteinMechanism()
mechanism.add(OptimalRubinsteinNegotiator())
mechanism.add(OptimalRubinsteinNegotiator())
print(f"Agreed to: {mechanism.run().agreement} in {mechanism.current_step} steps")

Agreed to: (0.5128205128205131, 0.4871794871794869) in 1 steps

We can see that even though both negotiators had the same time-pressure (\(\delta_0 = \delta_1\)) and have the same utility function, the negotiator that started, gets a higher utility at the equilibrium.

Let’s try to make an agent that does not use the information about the other agent’s

class AspirationRubinsteinNegotiator(RubinsteinNegotiator):
    def __init__(self, *args, aspiration_type="linear", max_aspiration=1.0, **kwargs):
        super().__init__(*args, **kwargs)
        self._asp = PolyAspiration(max_aspiration, aspiration_type)

    def propose(self, state: RubinsteinMechanismState)-> Outcome:
        if self.ufun((1.0, 1.0)) < 0.0:
            return None
        r = self._asp.utility_at(state.relative_time)
        return  (r, 1.0 - r) if self.my_index == 0 else (1.0 - r, r)

mechanism = RubinsteinMechanism(n_steps=100, extended=True)
mechanism.add(AspirationRubinsteinNegotiator())
mechanism.add(AspirationRubinsteinNegotiator())
result = mechanism.run()
print(f"Agreed to: {result.agreement} in {mechanism.current_step} steps")
plot_a_run(mechanism)

Agreed to: (0.49504950495049505, 0.49504950495049505) in 51 steps

Now we can see when the first negotiator is a conceder :

mechanism = RubinsteinMechanism(n_steps=100, extended=True)
mechanism.add(AspirationRubinsteinNegotiator(aspiration_type="conceder"))
mechanism.add(AspirationRubinsteinNegotiator())
print(f"Agreed to: {mechanism.run().agreement} in {mechanism.current_step} steps")
plot_a_run(mechanism)

Agreed to: (0.27438013387778515, 0.7227722772277227) in 28 steps

As expected, the agreement shifted toward the second agent.